Aprašomoji statistika, tai duomenų sisteminimo ir grafinio vaizdavimo metodai. Dažnai išsamus surinktos informacijos aprašymas bei duomenų grafikai leidžia daryti pagrįstas išvadas apie visos populiacijos nagrinėjamas savybes.
Aprašomoji statistika leidžia koncentruotai užrašyti informaciją, esančią dideliuose duomenų masyvuose. Todėl ji gali būti naudojama ir visos populiacijos duomenims apdoroti.
Jeigu skaičiuojant naudojami visos populiacijos duomenys, tai rezultatas vadinamas populiacijos parametru.
Jeigu skaičiuojant naudojami imties duomenys, tai rezultatas vadinamas imties statistika. Aprašomojoje statistikoje stebėjimo reikšmės pateikiamos lentelėmis, grafikais, dažnių skirstiniais arba charakteristikomis, susijusiomis su šiais skirstiniais.
Tarkime, kad stebimas tam tikras kintamasis. Populiaciją laikysime turinčia N elementų. Atsitiktinai išrinkę n elementų, sudarome kintamojo reikšmių statistinę eilutę:
x1, x2, …, xn, n ≤ N.
Išdėstyta nemažėjimo tvarka kiekybinio kintamojo duomenų eilutė x(1) ≤ x(2) ≤ x(3) ≤ … ≤ x(n) vadinama variacine eilute.
Skliausteliuose pažymėtas skaičius (j) vadinamas elemento eilės numeriu, o reikšmė x(j), (j = 1,2,3,…,n) – pozicinė statistika. Tada xmin = x(1), xmax = x(n).
Pvz. Gripo epidemijos metu buvo registruojamas ligonių skaičius 50-tyje šalies gyvenviečių. Iš šimto gyventojų gripu sirgo:
| 17 | 21 | 8 | 21 | 23 | 18 | 22 | 20 | 17 | 12 |
| 20 | 11 | 9 | 19 | 20 | 9 | 19 | 17 | 21 | 13 |
| 17 | 22 | 22 | 10 | 20 | 20 | 15 | 19 | 20 | 20 |
| 13 | 21 | 21 | 9 | 14 | 11 | 19 | 18 | 23 | 19 |
| 9 | 14 | 12 | 17 | 21 | 16 | 13 | 20 | 19 | 14 |
Variacinė eilutė bus tokia:
x(1)=8; x(2)=9; x(3)=9; x(4)=9; x(5)=9; x(6)=10; x(7)=11; x(8)=11; x(9)=12; x(10)=12; x(11)=13; x(12)=13; x(13)=13; x(14)=14; x(15)=14; x(16)=14; x(17)=15; x(18)=16; x(19)=17; x(20)=17; x(21)=17; x(22)=17; x(23)=17; x(24)=18; x(25)=18; x(26)=19; x(27)=19; x(28)=19; x(29)=19; x(30)=19; x(31)=19; x(32)=20; x(33)=20; x(34)=20; x(35)=20; x(36)=20; x(37)=20; x(38)=20; x(39)=20; x(40)=20; x(41)=21; x(42)=21; x(43)=21; x(44)=21; x(45)=21; x(46)=22; x(47)=22; x(48)=22; x(49)=23; x(50)=23.
Tarkime, kad vienu metu tiriami keli, sakykime, m kintamųjų. Tokiu atveju, tirdami n objektų, gauname n x m eilės duomenų matricą.
Dažniausiai tokia matrica išdėstoma šitaip: eilutėmis žymimi objektai, stulpeliais – kintamieji. Atskira eilutė vadinama stebiniu (realizacija).
Statistinėje eilutėje kintamojo x reikšmės gali kartotis. Tarkime, kad statistinėje eilutėje yra k skirtingų reikšmių ir jos yra x1,x2,…,xk. Sakykime, kad stebima reikšmė xj pasikartojo fj kartų.
Tuomet f1+f2+ . . . +fk = n, o xj statistinėje eilutėje sudaro fj /n dalį visų stebėjinių.
Kintamojo reikšmės dažnis fj – tai skaičius, nusakantis, kiek kartų reikšmė xj pasikartojo statistinėje eilutėje.
Kintamojo reikšmės santykinis dažnis fj /n – tai skaičius, nusakantis, kurią statistinės eilutės dalį sudaro xj.
Duomenims sisteminti dar naudojami sukauptieji dažniai, sukauptieji santykiniai dažniai.
| Reikšmė | x1 | x2 | x3 | … | xk |
| Dažnis | f1 | f2 | f3 | … | fk |
| Santykinis dažnis | f1/n | f2/n | f3/n | … | fk/n |
| Sukauptasis santykinis dažnis | f1/n | (f1+f2)/n | (f1+f2+f3)/n | … | (f1+…+fk)/n=1 |
Grupuotieji duomenys
Kai turime daug tolydžiojo kintamojo stebėjimų, dažnių lentelėje atsiranda labai daug skirtingų reikšmių. Tokius duomenis reikia grupuoti.
Prieš tai reikia nustatyti:
- grupavimo intervalų skaičių,
- jų plotį,
- intervalų kraštinius taškus.
Grupavimo intervalai
Grupavimo intervalų skaičius dažniausiai parenkama nuo 5 iki 15 intervalų.
Jeigu duomenų aibė gana simetriška, tai intervalų skaičių patariama rinktis pagal Sturgeso taisyklę:
k = 1+ 3,222 · log10n,
čia k – intervalų skaičius (sveikas skaičius), n – imties tūris.
Grupavimo intervalo ilgis
Grupavimo intervalo ilgį rekomenduojama pasirinkti pagal tokią formulę:
h = (xmax – xmin)/k,
čia xmax – maksimali imties reikšmė, xmin – minimali imties reikšmė.
Parenkant grupavimo intervalus yra priimama, kad grupavimo intervalų ilgiai yra vienodi, intervalai nesikerta, kiekviena kintamojo reikšmė patenka tik į vieną intervalą.
Pažymėkime i-tąjį grupavimo intervalą (ci-1, ci]. Tuomet fi – reikšmių, patekusių į intervalą (ci-1, ci], dažnis.
Grupuotų duomenų dažnių lentelė
Sugrupavus duomenis visa informacija surašoma į lentelę. Čia žymi intervalo (ci-1, ci] vidurio tašką.
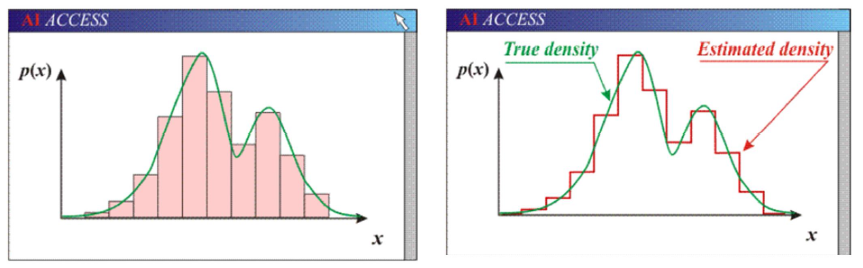
Tankio funkcija
Sisteminant kiekybinius duomenis, labai svarbi empirinio tankio funkcija.
Grupuotų duomenų empirinė tankio funkcija
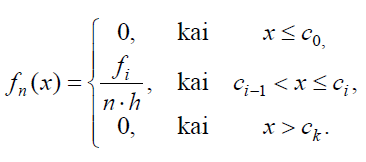
Kiekybiniams kintamiesiems galima apibrėžti ne tik dažnių skirstinį, bet ir dažnių (empirinę) pasiskirstymo funkciją.
Dažnių (empirinė) pasiskirstymo funkcija
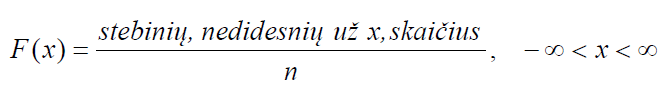
Dažnių pasiskirstymo funkcija atspindi visą sukauptąjį santykinį dažnį iki x.
Empirinė pasiskirstymo funkcija
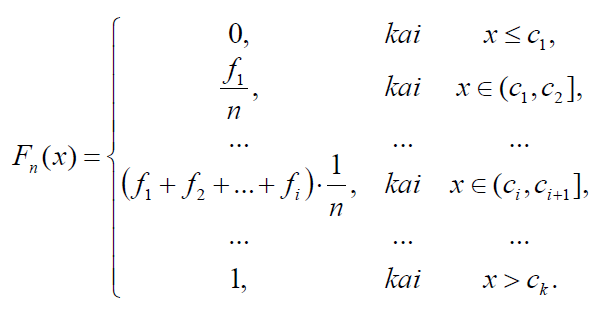
Dažnių skirstinio grafikai
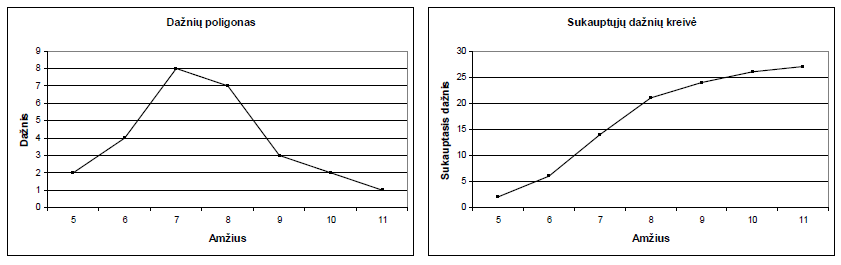
Paprasčiausias dažnių skirstinį iliustruojantis grafikas yra dažnių daugiakampis. Dažnių daugiakampis gaunamas Dekarto koordinatėse atidėtas dažnių reikšmes sujungus atkarpomis.
Dažniausiai braižoma sukauptųjų santykinių dažnių laužtė ar sukauptųjų procentų laužtė.
Tarkime, turime duomenis:
| Amžius | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Dažnis | 2 | 4 | 8 | 7 | 3 | 2 | 1 |
Histograma
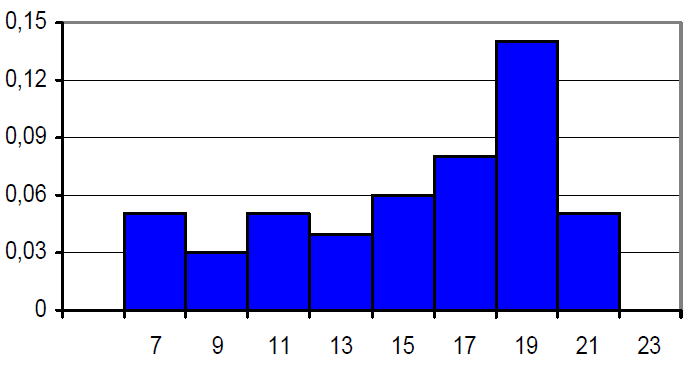
Empirinės grupuotų duomenų tankio funkcijos grafikas vadinamas histograma.
Histogramos braižymo procedūra:
- Ox ašyje atidedami grupavimo intervalai;
- kiekviename intervale braižomas stačiakampis, kurio aukštinė proporcinga pakliuvusiam į intervalą santykiniam dažniui ( fi/n arba fi/(nh)). Visų stačiakampių plotų suma turėtų būti lygi 1 (Tai yra reikalavimas, kad histograma turėtų tikimybinę interpretaciją).
Grupuotųjų duomenų pavyzdys
| Intervalai | Intervalo vidurys | Dažnis | Santykinis dažnis | Sukauptasis santykinis dažnis |
| (7;9] | 8 | 5 | 0,10 | 0,10 |
| (9;11] | 10 | 3 | 0,06 | 0,16 |
| (11;13] | 12 | 5 | 0,10 | 0,26 |
| (13;15] | 14 | 4 | 0,08 | 0,34 |
| (15;17] | 16 | 6 | 0,12 | 0,46 |
| (17;19] | 18 | 8 | 0,16 | 0,62 |
| (19;21] | 20 | 14 | 0,28 | 0,90 |
| (21;23] | 22 | 5 | 0,10 | 1 |
| >23 | 0 | 0 | 1 |
Empirinės pasiskirstymo funkcijos pavyzdys
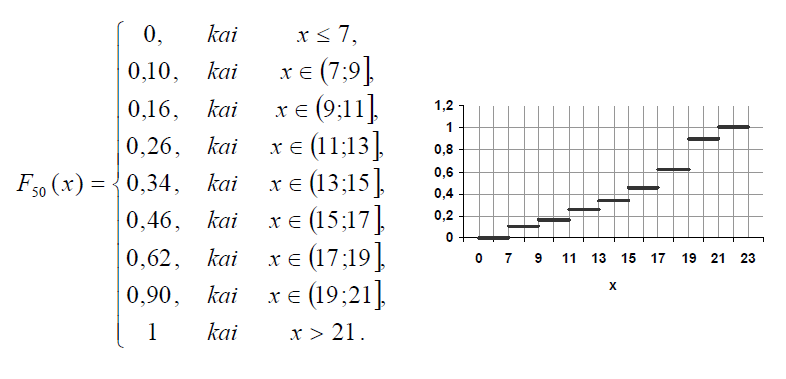
Tankio funkcijos pavyzdys
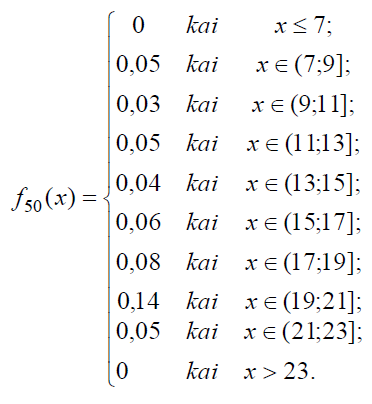
Histogramos pavyzdys
Histogramos pavyzdys