Tai charakteristikos, apibūdinančios duomenų ,,centrą”.
- Vidurkis.
- Mediana.
- Moda.
- Kvantiliai.
Visos charakteristikos, išskyrus modą, skaičiuojamos tik kiekybiniams duomenims.
Vidurkis
Vidurkis (average, mean) – tai taškas, kuris vidutiniškai artimiausias visiems statistinės eilutės elementams. Skaičiuojamas tik kiekybinių duomenų vidurkis.
Vidurkis yra labiausiai paplitusi duomenų padėties charakteristika – yra skaičiuojamas vidutinis darbo užmokestis, sesijos įvertinimų vidurkis, vidutinės kainos ir pan.
Imties vidurkis
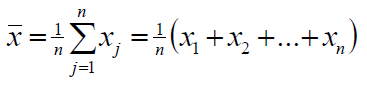
Populiacijos vidurkis
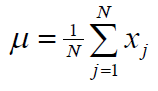
Grupuotų duomenų vidurkis
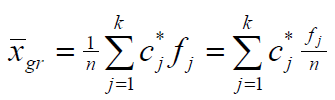
Vidurkio savybės
- Pasinaikinimo efektas:
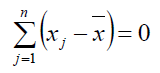
- Visas stebinių reikšmes padauginus iš to paties skaičiaus, gautas aritmetinis vidurkis taip pat bus padaugintas iš šio skaičiaus:
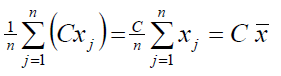
- Pridėjus (atėmus) prie kiekvieno stebinio tam tikrą skaičių, vidurkis padidės (sumažės) tokiu pat skaičiumi:
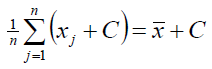
Vidurkio naudojimo trūkumai
Jei statistinėje eilutėje yra labai išsiskiriančios iš kitų stebinių reikšmės (labai didelės arba labai mažos), vidurkis nėra itin geras matas, nesneatspindi to, kas būdinga daugumai stebėjimų.
Pavyzdžiui, pakėlus keletą kartų atlyginimą vienam darbuotojui, tuo pačiu padidėja ir vidutinis atlyginimas, nors kitų darbuotojų atlyginimai ir nesikeitė.
Vidurkio pavyzdys
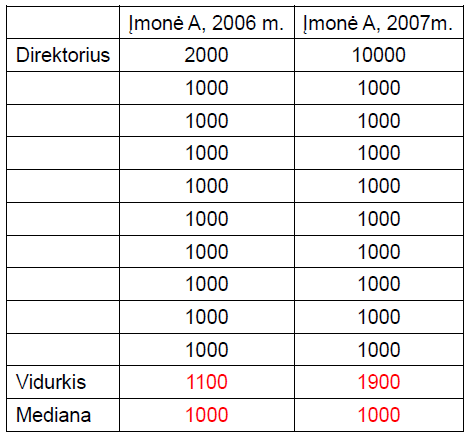
Mediana
Imties mediana (Median) yra skaičius, už kurį 50 variacinės eilutės reikšmių yra ne didesnės ir 50 ne mažesnės. Mediana – tai skaičius, perskiriantis variacinę eilutę į dvi maždaug lygias dalis.
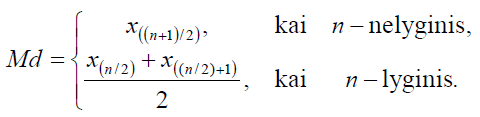
Kaip ir aritmetinis vidurkis, mediana charakterizuoja duomenų centrą. Patariama naudoti, kai duomenų aibėje yra išskirčių. Dažniausiai naudojama ranginiams ir intervaliniams duomenims.
Grupuotiems duomenims mediana paskaičiuojama taip: visos į intervalą patekusias reikšmes pakeičiamos vidurinėmis reikšmėmis ir tada pritaikoma medianos skaičiavimo formulė.
Moda
Ne visada vidurkis yra pati tinkamiausia charakteristika. Dar viena duomenų padėties charakteristika yra moda (mode).
Moda (Mo) – dažniausiai aibėje pasirodanti reikšmė.
Sugrupuotiems duomenims moda yra lygi didžiausio dažnio intervalo viduriui.
Pvz. Turime variacinę eilutę: 8, 12, 15, 15, 18, 20, 20, 20, 22, 24, 27, Variacinėje eilutėje daugiausiai kartų pasikartoja reikšmė lygi 20. Taigimoda Mo = 20.
Moda ypač naudinga atvejais, kai vidurkis bei mediana nėra lengvai apibrėžiami, pavyzdžiui, aibės {bulvė, bulvė, morka, ridikas, ridikas, ridikas, svogūnas} moda yra reikšmė ‘ridikas’.
Jeigu visos reikšmės statistinėje eilutėje pasikartoja vienodai dažnai, sakoma, kad pasiskirstymas modos neturi. Jei yra dvi negretimos reikšmės, kurių dažniai vienodi ir didžiausi, skirstinys vadinamas bimodiniu. Jei jos yra gretimos, skaičiuojamas jų aritmetinis vidurkis kaip viena moda.
Modų gali būti ir daugiau, negu dvi. Kai moda viena, skirstinys vadinamas unimodiniu. Jei modų daug, skirstinys vadinamas multimodiniu. Modos skaičiuojamos tiek kokybiniams, tiek kiekybiniams duomenims.
Kvantiliai
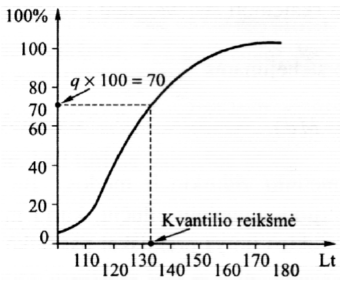 Reikšmė, dalijanti variacinę eilutę į q·100 ir (1–q)·100 procentinių dalių, vadinama q-tosios eilės kvantiliu (quantile) (0 < q < 1).
Reikšmė, dalijanti variacinę eilutę į q·100 ir (1–q)·100 procentinių dalių, vadinama q-tosios eilės kvantiliu (quantile) (0 < q < 1).
Kvantilio radimas:
- Randamas indeksas: i= q·n.
- Jei i nėra sveikas skaičius, tai imama jo sveikoji dalis. Ieškomas kvantilis yra [i]+1 variacinės eilutės narys.
- Jei i sveikas skaičius, tai ieškomas kvantilis i ir i+1 variacinės eilutės narių aritmetinis vidurkis.
Kvartiliai
Dydžiai, dalijantys variacinę eilutę į keturias maždaug lygias dalis yra vadinamo kvartiliais (quartile). Žymimi Q1, Q2, Q3. Antrasis kvartilis sutampa su mediana Q2= Md. Q1 dar vadinamas apatiniu (lower) kvartiliu, o Q3 – viršutiniu (upper) kvartiliu.


Kodėl nėra įvardinta ką. Kas reiškia., ir uždavinių sprendimo būdų.